JDK源码阅读之PriorityBlockingQueue

发表于 | 分类于 | 评论数： | 阅读次数：

写在前面

An unbounded {@linkpain java.util.concurrent.BlockingQueue blocking queue} that uses the same ordering rules as class {@link PriorityQueue} and supplies blocking retrieval operations.

源码分析自 JDK 1.8.0_171
PriorityBlockingQueue,无界优先级阻塞队列。队列中的优先级根据提供的独立的一个 Comparator 接口或者实现 Comparable 接口的队列元素决定。

概述

优先级队列是基于堆(小顶堆)是实现的。线程安全性由内部声明的一个ReentrantLock保证，即所有的公共操作都是在锁下完成。

堆

堆实际上是一种完全二叉树，分为大顶堆和小顶堆。大顶堆的堆顶的关键字肯定是所有关键字中最大的，小顶堆的堆顶的关键字是所有关键字中最小的。如下图：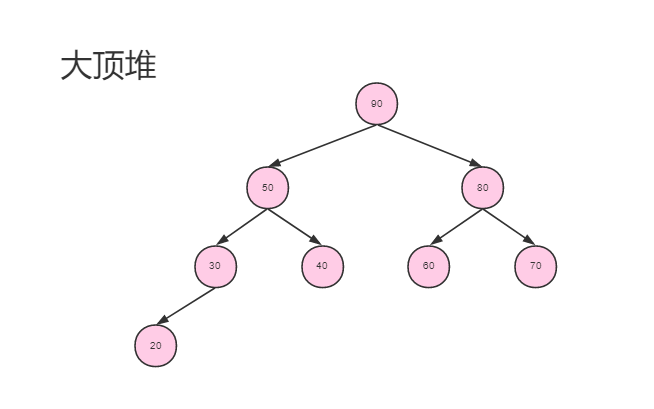
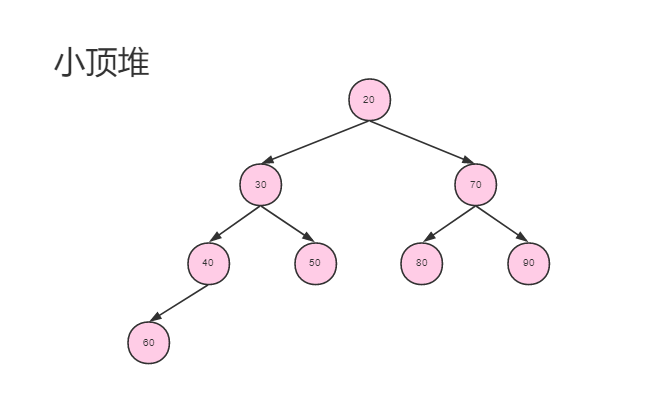
big.jpgsmall.jpg

一般堆都是由数组实现，记一个节点的索引下标为n，那么它的左右孩子为 2n+1 和 2(n+1) 。

内部变量

  • private static final int DEFAULT_INITIAL_CAPACITY = 11; // 默认数组大小
  • private static final int MAX_ARRAY_SIZE = Integer.MAX_VALUE - 8; // 数组支持最大大小
  • private transient Object[] queue; // 存储元素底层数组，以堆的形式
  • private transient int size; // 队列中元素数量
  • private transient Comparator<? super E> comparator; // 用于区分优先级的比较接口
  • private final ReentrantLock lock; // 保证线程安全的锁
  • private final Condition notEmpty; // lock.condition
  • private transient volatile int allocationSpinLock; // 用于数组扩展时的自旋锁

构造方法

  • public PriorityBlockingQueue();
1
2
3
4
5
6
7
8
/**
    * Creates a {@code PriorityBlockingQueue} with the default
    * initial capacity (11) that orders its elements according to
    * their {@linkplain Comparable natural ordering}.
    */
   public PriorityBlockingQueue() {
       this(DEFAULT_INITIAL_CAPACITY, null);
   }

队列默认大小为11
**

  • public PriorityBlockingQueue(int initialCapacity);
1
2
3
4
5
6
7
8
9
10
11
12
/**
    * Creates a {@code PriorityBlockingQueue} with the specified
    * initial capacity that orders its elements according to their
    * {@linkplain Comparable natural ordering}.
    *
    * @param initialCapacity the initial capacity for this priority queue
    * @throws IllegalArgumentException if {@code initialCapacity} is less
    *         than 1
    */
   public PriorityBlockingQueue(int initialCapacity) {
       this(initialCapacity, null);
   }

未传入comparator，则需要队列元素自身实现ComParable接口

  • public PriorityBlockingQueue(int initialCapacity,Comparator<? super E> comparator);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
/**
    * Creates a {@code PriorityBlockingQueue} with the specified initial
    * capacity that orders its elements according to the specified
    * comparator.
    *
    * @param initialCapacity the initial capacity for this priority queue
    * @param  comparator the comparator that will be used to order this
    *         priority queue.  If {@code null}, the {@linkplain Comparable
    *         natural ordering} of the elements will be used.
    * @throws IllegalArgumentException if {@code initialCapacity} is less
    *         than 1
    */
   public PriorityBlockingQueue(int initialCapacity,
                                Comparator<? super E> comparator) {
       if (initialCapacity < 1)
           throw new IllegalArgumentException();
       this.lock = new ReentrantLock();
       this.notEmpty = lock.newCondition();
       this.comparator = comparator;
       this.queue = new Object[initialCapacity];
   }
  • public PriorityBlockingQueue(Collection<? extends E> c);
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
/**
    * Creates a {@code PriorityBlockingQueue} containing the elements
    * in the specified collection.  If the specified collection is a
    * {@link SortedSet} or a {@link PriorityQueue}, this
    * priority queue will be ordered according to the same ordering.
    * Otherwise, this priority queue will be ordered according to the
    * {@linkplain Comparable natural ordering} of its elements.
    *
    * @param  c the collection whose elements are to be placed
    *         into this priority queue
    * @throws ClassCastException if elements of the specified collection
    *         cannot be compared to one another according to the priority
    *         queue's ordering
    * @throws NullPointerException if the specified collection or any
    *         of its elements are null
    */
   public PriorityBlockingQueue(Collection<? extends E> c) {
       this.lock = new ReentrantLock();
       this.notEmpty = lock.newCondition();
       boolean heapify = true; // true if not known to be in heap order
       boolean screen = true;  // true if must screen for nulls
       if (c instanceof SortedSet<?>) {
           SortedSet<? extends E> ss = (SortedSet<? extends E>) c;
           this.comparator = (Comparator<? super E>) ss.comparator();
           heapify = false;
       }
       else if (c instanceof PriorityBlockingQueue<?>) {
           PriorityBlockingQueue<? extends E> pq =
               (PriorityBlockingQueue<? extends E>) c;
           this.comparator = (Comparator<? super E>) pq.comparator();
           screen = false;
           if (pq.getClass() == PriorityBlockingQueue.class) // exact match
               heapify = false;
       }
       Object[] a = c.toArray();
       int n = a.length;
       // If c.toArray incorrectly doesn't return Object[], copy it.
       if (a.getClass() != Object[].class)
           a = Arrays.copyOf(a, n, Object[].class);
       if (screen && (n == 1 || this.comparator != null)) {
           for (int i = 0; i < n; ++i)
               if (a[i] == null)
                   throw new NullPointerException();
       }
       this.queue = a;
       this.size = n;
       if (heapify)
           heapify();
   }

有必要的话，需要堆化

源码分析

PriorityBlockingQueue的最主要的两个动作时，往队列中放入元素，从队列中取出元素。对应的两个核心的方法时 offer 和 poll 。此外还有在上述其中一个构造方法中，设计到一个堆化的操作，对应的方法时 heapify 。

heapify

以堆的形式重新组织数组中的元素。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
/**
    * Establishes the heap invariant (described above) in the entire tree,
    * assuming nothing about the order of the elements prior to the call.
    */
   private void heapify() {
       Object[] array = queue;
       int n = size;
       // 因为堆的特性，所以，只需要从half位置开始往前搜刮
       int half = (n >>> 1) - 1;
       Comparator<? super E> cmp = comparator;
       if (cmp == null) {
           for (int i = half; i >= 0; i--)
               // 位置i往后的孩子们不用担心了，已经拍好队了
               // i向下找array[i]的位置
               siftDownComparable(i, (E) array[i], array, n);
       }
       else {
           for (int i = half; i >= 0; i--)
               // 同理
               siftDownUsingComparator(i, (E) array[i], array, n, cmp);
       }
   }

offer

队列是无界的，所以理论上offer永远返回true。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
    * Inserts the specified element into this priority queue.
    * As the queue is unbounded, this method will never return {@code false}.
    *
    * @param e the element to add
    * @return {@code true} (as specified by {@link Queue#offer})
    * @throws ClassCastException if the specified element cannot be compared
    *         with elements currently in the priority queue according to the
    *         priority queue's ordering
    * @throws NullPointerException if the specified element is null
    */
   public boolean offer(E e) {
       if (e == null)
           throw new NullPointerException();
       final ReentrantLock lock = this.lock;
       lock.lock();
       int n, cap;
       Object[] array;
       // size超过了数组大小，就需要扩容了
       while ((n = size) >= (cap = (array = queue).length))
           tryGrow(array, cap);
       try {
           Comparator<? super E> cmp = comparator;
           if (cmp == null)
               // 从位置n开始往上找到合适e待的位置，被e替换下的元素放在n位置上
               siftUpComparable(n, e, array);
           else
               // 同理
               siftUpUsingComparator(n, e, array, cmp);
           // 容量 +1
           size = n + 1;
           // signal 阻塞的get线程
           notEmpty.signal();
       } finally {
           lock.unlock();
       }
       return true;
   }

扩容的时候有点讲究，见下

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
/**
    * Tries to grow array to accommodate at least one more element
    * (but normally expand by about 50%), giving up (allowing retry)
    * on contention (which we expect to be rare). Call only while
    * holding lock.
    *
    * @param array the heap array
    * @param oldCap the length of the array
    */
   private void tryGrow(Object[] array, int oldCap) {
       // 释放锁，用自旋锁保证安全性
       lock.unlock(); // must release and then re-acquire main lock
       Object[] newArray = null;
       if (allocationSpinLock == 0 &&
               // 扩容时，用自旋锁锁住
           UNSAFE.compareAndSwapInt(this, allocationSpinLockOffset,
                                    0, 1)) {
           try {
               // 如果当前容量小于64，则每次扩容2，否则往两倍扩
               int newCap = oldCap + ((oldCap < 64) ?
                                      (oldCap + 2) : // grow faster if small
                                      (oldCap >> 1));
               if (newCap - MAX_ARRAY_SIZE > 0) {    // possible overflow
                   int minCap = oldCap + 1;
                   if (minCap < 0 || minCap > MAX_ARRAY_SIZE)
                       throw new OutOfMemoryError();
                   newCap = MAX_ARRAY_SIZE;
               }
               if (newCap > oldCap && queue == array)
                   newArray = new Object[newCap];
           } finally {
               allocationSpinLock = 0;
           }
       }
       if (newArray == null) // back off if another thread is allocating
           Thread.yield();
       // 重新获取锁
       lock.lock();
       if (newArray != null && queue == array) {
           queue = newArray;
           System.arraycopy(array, 0, newArray, 0, oldCap);
       }
   }

poll

需要在持有锁的前提下，才能从队列中获取元素。获取元素成功后，原则上堆结构是被_破坏_了，所以需要重新调整堆结构。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
public E poll() {
       final ReentrantLock lock = this.lock;
       // 需要持有锁
       lock.lock();
       try {
           // 出队
           return dequeue();
       } finally {
           lock.unlock();
       }
   }

   /**
    * Mechanics for poll().  Call only while holding lock.
    */
   private E dequeue() {
       int n = size - 1;
       if (n < 0)
           return null;
       else {
           Object[] array = queue;
           // 堆顶元素
           E result = (E) array[0];
           E x = (E) array[n];
           array[n] = null;
           Comparator<? super E> cmp = comparator;
           if (cmp == null)
               // 调整堆结构，即从位置0往下找x的位置
               siftDownComparable(0, x, array, n);
           else
               siftDownUsingComparator(0, x, array, n, cmp);
           // size -= 1
           size = n;
           return result;
       }
   }

调整堆

上文提到的调整堆的操作有 siftDownComparable(siftDownUsingComparator) 和 siftUpComparable(siftUpUsingComparator) 。siftDownComparable 和 siftDownUsingComparator 是同一种操作，只是比较元素大小一个是利用元素实现 Comparable 接口，一个是利用构造时传入的 Comparator 。

siftDownComparable
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
/**
    * Inserts item x at position k, maintaining heap invariant by
    * demoting x down the tree repeatedly until it is less than or
    * equal to its children or is a leaf.
    *
    * @param k the position to fill
    * @param x the item to insert
    * @param array the heap array
    * @param n heap size
    */
   private static <T> void siftDownComparable(int k, T x, Object[] array,
                                              int n) {
       if (n > 0) {
           Comparable<? super T> key = (Comparable<? super T>)x;
           int half = n >>> 1;           // loop while a non-leaf
           // k < half 只需数组的前半段找
           while (k < half) {
               // 左孩子 2n+1
               int child = (k << 1) + 1; // assume left child is least
               Object c = array[child];
               // 右孩子 2(n+1)
               int right = child + 1;
               if (right < n &&
                   ((Comparable<? super T>) c).compareTo((T) array[right]) > 0)
                   // 找到最小的孩子
                   c = array[child = right];
               if (key.compareTo((T) c) <= 0)
                   // 如果key比最小的孩子还小，那么表示key的位置就是这里,break
                   break;
               // key应该放在最小的孩子的位置
               array[k] = c;
               // 然后继续找替换掉孩子的位置
               k = child;
           }
           // 这是k应该是父 而key是比k的孩子都小
           array[k] = key;
       }
   }

siftUpComparable
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
/**
    * Inserts item x at position k, maintaining heap invariant by
    * promoting x up the tree until it is greater than or equal to
    * its parent, or is the root.
    *
    * To simplify and speed up coercions and comparisons. the
    * Comparable and Comparator versions are separated into different
    * methods that are otherwise identical. (Similarly for siftDown.)
    * These methods are static, with heap state as arguments, to
    * simplify use in light of possible comparator exceptions.
    *
    * @param k the position to fill
    * @param x the item to insert
    * @param array the heap array
    */
   private static <T> void siftUpComparable(int k, T x, Object[] array) {
       Comparable<? super T> key = (Comparable<? super T>) x;
       while (k > 0) {
           // 父节点
           int parent = (k - 1) >>> 1;
           Object e = array[parent];
           if (key.compareTo((T) e) >= 0)
               // 要是比父节点大，则跳出，表示x应该放在k处
               break;
           // 比父节点小，则顶替父节点
           array[k] = e;
           // 接着网上找父节点的位置
           k = parent;
       }
       // 填充k位置
       array[k] = key;
   }

总结

优先级队列内部数据结构是一个数组，这个数组是以堆的形式组织的。线程安全性由内部的一个 ReentrantLock 保证，所有对元素的公共操作是需要在持有锁的前提下才能完成。

出入队后，我们说这个堆结构是被破坏了，所以需要重新调整下这个堆结构。调整堆主要是由两个操作组成：siftUp[Comparable|Comparator] 和 siftDown[Comparable|Comparator] 。分别是从下往上找替换的元素位置，从上往下找替换元素的位置。

-------------The End-------------