JDK源码阅读之TreeMap

发表于 | 分类于 | 评论数： | 阅读次数：

写在前面

A Red-Black tree based NavigableMa implementation.

TreeMap，是一种具有排序功能的 Map ，是一种基于红黑树结构的的 NavigableMap 。由于它具有红黑树的结构，所以它的 get 、 put 、 constainsKey 、remove等操作能够保证在log(n)的时间复杂度。

红黑树

TreeMap是基于红黑树实现的一种 NavigableMap。红黑树是一种二叉搜索树，具有以下性质：

  • 性质1 树上的节点要么是红色要么是黑色
  • 性质2 根节点一定是黑色
  • 性质3 树上不存在连续的红色节点
  • 性质4 任一根到叶子节点路径上具有相同数目的黑色节点

无论是往红黑树上添加节点还是移除节点，都需要进行必要的balance，以保证以上四条性质不被破坏。
往树上添加节点和移除节点的balance策略是不尽相同的，各自都需要分多钟情况讨论。
在对这两种情况展开讨论之前，先说明两个操作，即 左旋 和 右旋:

左旋

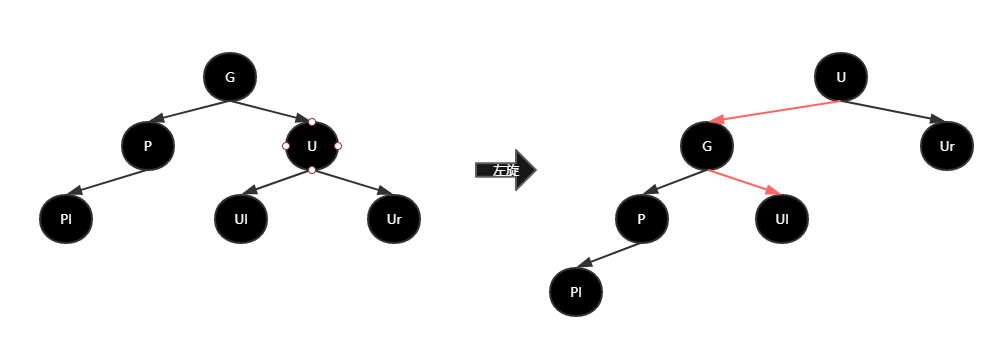
left_oritate.jpg
如上图，对G左旋，G原本的右孩子U，成为G的父节点，G成为U的左孩子，U原本的左孩子Ul成为G的右孩子。

右旋

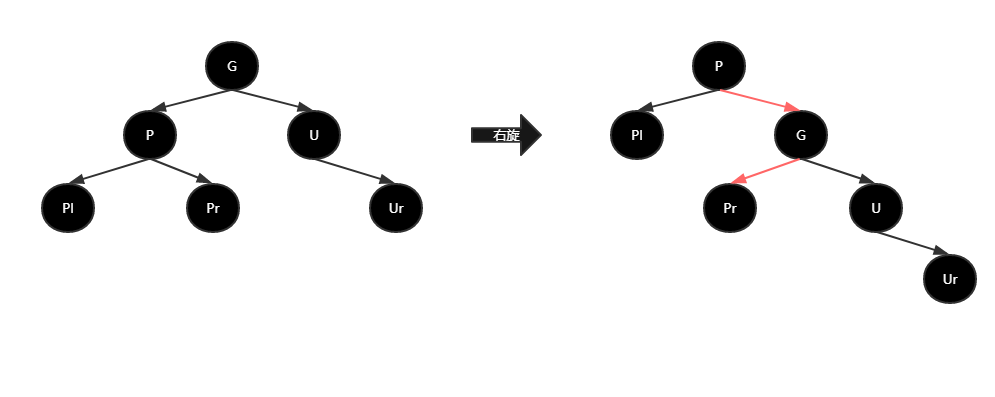
right_oritate.jpg
如上图，对G右旋，P成为父节点，G为P的右孩子，P原本的右孩子Pr，挪为G的左孩子。

添加节点

节点上的节点要么是红色要么是黑色，那么添加的节点应该选择哪种颜色呢？答案应该是红色，应为如果是黑色，那么 性质4 就被破坏了，所以为了避免复杂性，应该设定添加的节点颜色为红色。

假设要往树上 P 下添加节点 N ， P 的兄弟节点为 U ， 父节点为 G 。如图：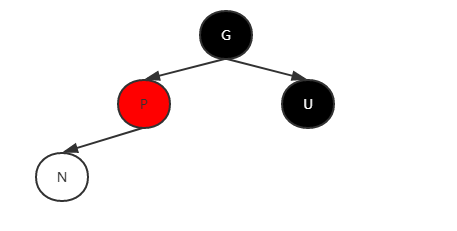
red_black_tree_insert.jpg

以上图为例，在插入节点时做以下情况说明：

  • 情况一 N 是头结点。则从red变色为black
  • 情况二 N 的父节点P是黑色。则不用调整
  • 情况三 N 的父节点P是红色，叔叔节点U也为红色。P、U -> black; then G -> red;可能需要往上递归处理，因为可能存在连续的红色节点,如果G是root，则需要将其颜色置为black
  • 情况四 N 的父节点P是红色，叔叔节点U为黑色，且N是P的左孩子。则P、G互换颜色，然后对G右旋
  • 情况五 N 的父节点P是红色，叔叔节点U为黑色，且N为P的右孩子。则对P先左旋，然后按 情况四 处理

插入的情况一共就以上五种情况，可以自己画一画加深印象。

移除节点

移除节点的流程一般是这样: 直接删除，找到前驱(删除节点左子树上的最大节点)或后继(删除节点右子树上的最小节点)，将找到的前驱或后继赋值到删除节点，最后删除前驱或者后继,因为前驱或后继至多只有一个孩子，因此问题简化为删除至多只有一个孩子的问题。
delete_origin.jpg

移除节点的情况就先对复杂一些了，以上图为例分情况说明:

  • 情况一 移除节点 X 为red。则由唯一的孩子顶替即可(红黑树的四个原则并没有遭到破坏)
  • 情况二 删除节点是black，path上少了个black节点，分为两种大的情况：
    • s1： 待删除节点唯一的孩子为红色，则直接顶替并变色即可
    • s2： 待删除节点唯一的孩子为黑色，需要分为6中情况(以上图例子说明)：
      • s2.1：删除节点为根节点,则子节点直接替换父节点
      • s2.2：N 父节点G为red,兄弟节点s及其孩子均为black，少了个black x，即N路径上少了个黑，则父节点和兄弟节点换个颜色
      • s2.3：N 的父节点G可red可black,兄弟节点s为black,s的左孩子SL为可red可black,s的右孩子SR为red，则1.对G左旋；2.再G和S互换颜色，SL移为N的右孩子，SR改变颜色为black
      • s2.4：N 的父节点G可red可black,兄弟节点s为black，s的左孩子SL为red，s的右孩子SR为black，则对S右旋，且S和SL互换颜色，则变成情况3
      • s2.5：N 的兄弟节点S为red,其他节点为黑色，则G和S互换颜色, 对G左旋，这个时候左子树(照具体情况按情况2 3 4处理)
      • s2.6：N 的父节点，兄弟节点及其兄弟孩子节点均为black,则将S变为red，这时按情况5处理

源码分析

TreeMap的类声明如下:

1
2
3
4
5
public class TreeMap<K, V>
        extends AbstractMap<K, V>
        implements NavigableMap<K, V>, Cloneable, Serializable {

    }

可知TreeMap具有Map的一般行为，同是也是NavigableMap。

变量

  • private final Comparator<? super K> comparator; // 用于元素排序的比较器
  • private transient Entry<K, V> root; // 红黑树的root
  • private transient int size = 0; // 目前红黑树中容纳的元素个数
  • private transient int modCount = 0; // 修改计数，failfast
  • private static final boolean RED = false; // 红色
  • private static final boolean BLACK = true; // 黑色

    构造方法

1
2
3
public TreeMap() {
        comparator = null;
    }

默认构造方法并没有初始化任何变量，包括树的首尾(并不需要一般链表中的dummy node)

1
2
3
public TreeMap(Comparator<? super K> comparator) {
        this.comparator = comparator;
    }

带一个维护内部元素顺序的比较器参数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
public TreeMap(SortedMap<K, ? extends V> m) {
        comparator = m.comparator();
        try {
            buildFromSorted(m.size(), m.entrySet().iterator(), null, null);
        } catch (java.io.IOException cannotHappen) {
        } catch (ClassNotFoundException cannotHappen) {
        }
    }

    private void buildFromSorted(int size, Iterator<?> it,
                                 java.io.ObjectInputStream str,
                                 V defaultVal)
            throws java.io.IOException, ClassNotFoundException {
        this.size = size;
        root = buildFromSorted(0, 0, size - 1, computeRedLevel(size),
                it, str, defaultVal);
    }

    /**
    * 迭代构造红黑树
    */
    private final Entry<K, V> buildFromSorted(int level, int lo, int hi,
                                              int redLevel,
                                              Iterator<?> it,
                                              java.io.ObjectInputStream str,
                                              V defaultVal)
            throws java.io.IOException, ClassNotFoundException {
        /*
         * Strategy: The root is the middlemost element. To get to it, we
         * have to first recursively construct the entire left subtree,
         * so as to grab all of its elements. We can then proceed with right
         * subtree.
         *
         * The lo and hi arguments are the minimum and maximum
         * indices to pull out of the iterator or stream for current subtree.
         * They are not actually indexed, we just proceed sequentially,
         * ensuring that items are extracted in corresponding order.
         */

        if (hi < lo) return null;

        int mid = (lo + hi) >>> 1;

        Entry<K, V> left = null;
        if (lo < mid)
            // 迭代建左子树
            left = buildFromSorted(level + 1, lo, mid - 1, redLevel,
                    it, str, defaultVal);

        // extract key and/or value from iterator or stream
        K key;
        V value;
        if (it != null) {
            if (defaultVal == null) {
                java.util.Map.Entry<?, ?> entry = (java.util.Map.Entry<?, ?>) it.next();
                key = (K) entry.getKey();
                value = (V) entry.getValue();
            } else {
                key = (K) it.next();
                value = defaultVal;
            }
        } else { // use stream
            key = (K) str.readObject();
            value = (defaultVal != null ? defaultVal : (V) str.readObject());
        }

        Entry<K, V> middle = new Entry<>(key, value, null);

        // color nodes in non-full bottommost level red
        if (level == redLevel)
            // 默认RED节点在最底层(non-full)
            middle.color = RED;

        if (left != null) {
            middle.left = left;
            left.parent = middle;
        }

        if (mid < hi) {
            Entry<K, V> right = buildFromSorted(level + 1, mid + 1, hi, redLevel,
                    it, str, defaultVal);
            middle.right = right;
            right.parent = middle;
        }

        return middle;
    }

    /* 初始化时，计算红色节点所在层级，红色节点在最底层 */
    private static int computeRedLevel(int sz) {
        int level = 0;
        // 找到black node的层级
        for (int m = sz - 1; m >= 0; m = m / 2 - 1) // 第n层的节点，左右孩子索引分别为 2n+1 和 2(n+1)，所以才有 m=m/2-1
            level++;
        return level;
    }

要是传入的是一个已经有序的Map，那么可以根据这个Map迭代构造红黑树

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
public TreeMap(java.util.Map<? extends K, ? extends V> m) {
        comparator = null;
        putAll(m);
    }

    public void putAll(java.util.Map<? extends K, ? extends V> map) {
        int mapSize = map.size();
        if (size == 0 && mapSize != 0 && map instanceof SortedMap) {    // 参数map内的元素要求是有序的
            Comparator<?> c = ((SortedMap<?, ?>) map).comparator();
            if (c == comparator || (c != null && c.equals(comparator))) {
                ++modCount;
                try {
                    buildFromSorted(mapSize, map.entrySet().iterator(),
                            null, null);
                } catch (java.io.IOException cannotHappen) {
                } catch (ClassNotFoundException cannotHappen) {
                }
                return;
            }
        }
        super.putAll(map);
    }

要是Map是个有的Map，则在构造时建立红黑树(同上一情况)，否则等到第一次对树上元素操作时才会处理

一般行为

  • rotateLeft 左旋
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
private void rotateLeft(Entry<K, V> p) {
        if (p != null) {
            Entry<K, V> r = p.right;

            // p的右孩子r的左孩子挪到p的right
            p.right = r.left;
            if (r.left != null) r.left.parent = p;

            // p的右孩子r顶替p的位置
            r.parent = p.parent;
            if (p.parent == null)
                root = r;
            else if (p.parent.left == p)    // p为左孩子
                p.parent.left = r;
            else
                p.parent.right = r; // p为右孩子

            // p成为r的左孩子
            r.left = p;
            p.parent = r;
        }
    }
  • rotateRight 右旋
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
private void rotateRight(Entry<K, V> p) {
        if (p != null) {
            Entry<K, V> l = p.left;

            // p的左孩子l的右孩子挪到p的left
            p.left = l.right;
            if (l.right != null) l.right.parent = p;

            // p的左孩子l顶替p的位置
            l.parent = p.parent;
            if (p.parent == null)
                root = l;
            else if (p.parent.right == p)   // p为右孩子
                p.parent.right = l;
            else p.parent.left = l; // p为左孩子

            // p成为l的右孩子
            l.right = p;    // p成为左孩子l的右孩子
            p.parent = l;   // 左孩子l成为p的parent
        }
    }
  • predecessor 前驱
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
static <K, V> Entry<K, V> predecessor(Entry<K, V> t) {
        /* 前驱 */
        if (t == null)
            return null;
        else if (t.left != null) {
            // 左子树的最右(大)节点
            Entry<K, V> p = t.left;
            while (p.right != null)
                p = p.right;
            return p;
        } else {
            // t无左子树，前驱只能从向上找，t为predecessor的右子树的最左(小)节点
            Entry<K, V> p = t.parent;
            Entry<K, V> ch = t;
            while (p != null && ch == p.left) {
                ch = p;
                p = p.parent;
            }
            return p;
        }
    }
  • successor 后继
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
static <K, V> Entry<K, V> successor(Entry<K, V> t) {
        /* 后继 */

        if (t == null)
            return null;
        else if (t.right != null) {
            // 右子树的最左(小)节点
            Entry<K, V> p = t.right;
            while (p.left != null)
                p = p.left;
            return p;
        } else {
            // t无右子树，后继只能从上找，t为successor的左子树的最右(大)节点
            Entry<K, V> p = t.parent;
            Entry<K, V> ch = t;
            while (p != null && ch == p.right) {    // ch == p.right 即ch为右孩子
                ch = p;
                p = p.parent;
            }
            return p;
        }
    }
  • getLastEntry
1
2
3
4
5
6
7
8
final Entry<K, V> getLastEntry() {
        Entry<K, V> p = root;
        if (p != null)
            // 树的最右节点，最大
            while (p.right != null)
                p = p.right;
        return p;
    }
  • getFirstEntry
1
2
3
4
5
6
7
8
final Entry<K, V> getFirstEntry() {
        Entry<K, V> p = root;
        if (p != null)
            // 树的最左节点，最小
            while (p.left != null)
                p = p.left;
        return p;
    }
  • getEntry
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
final Entry<K, V> getEntry(Object key) {
        // Offload comparator-based version for sake of performance
        if (comparator != null)
            return getEntryUsingComparator(key);
        if (key == null)
            throw new NullPointerException();
        @SuppressWarnings("unchecked")
        Comparable<? super K> k = (Comparable<? super K>) key;
        Entry<K, V> p = root;
        while (p != null) {
            int cmp = k.compareTo(p.key);
            if (cmp < 0)
                p = p.left; // 小于则在左子树上找
            else if (cmp > 0)
                p = p.right;    // 大于则在右子树上找
            else
                return p;
        }
        return null;
    }

put

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
public V put(K key, V value) {
        Entry<K, V> t = root;
        // 根节点为null,则直接插入
        if (t == null) {
            compare(key, key); // type (and possibly null) check

            root = new Entry<>(key, value, null);   // attention! 颜色为black
            size = 1;
            modCount++;
            return null;
        }
        int cmp;
        Entry<K, V> parent;
        // split comparator and comparable paths
        Comparator<? super K> cpr = comparator;
        if (cpr != null) {
            do {
                parent = t; // 找到<key,value>的parent
                cmp = cpr.compare(key, t.key);
                if (cmp < 0)
                    // key < t.key value应在左子树上
                    t = t.left;
                else if (cmp > 0)
                    // key> t.key value应在右子树上
                    t = t.right;
                else
                    // 存在相同的key则替换
                    return t.setValue(value);
            } while (t != null);    // t应该是插入节点的parent
        } else {
            if (key == null)
                throw new NullPointerException();
            @SuppressWarnings("unchecked")
            Comparable<? super K> k = (Comparable<? super K>) key;
            do {
                parent = t;
                cmp = k.compareTo(t.key);
                if (cmp < 0)
                    t = t.left;
                else if (cmp > 0)
                    t = t.right;
                else
                    return t.setValue(value);
            } while (t != null);
        }
        Entry<K, V> e = new Entry<>(key, value, parent);    // 目前e的颜色为black
        if (cmp < 0)
            // e < parent.key 插在左子树上
            parent.left = e;
        else
            // e > parent.key 插在右子树上
            parent.right = e;
        // 插入节点后需要平衡
        fixAfterInsertion(e);
        size++;
        modCount++;
        return null;
    }

    /**
     * From CLR 插入后的平衡
     */
    private void fixAfterInsertion(Entry<K, V> x) {
        x.color = RED;  // 插入的节点必须为RED

        // s1: x为头结点则变色(red-> black)即可
        // s2: x.parent==black ，不用调整
        while (x != null && x != root && x.parent.color == RED) {
            // 对照上述列举的插入节点的五种情况:

            // x.parent == x.parent.parent.left x.parent为左孩子
            if (parentOf(x) == leftOf(parentOf(parentOf(x)))) {
                Entry<K, V> y = rightOf(parentOf(parentOf(x))); // y = x.parent.parent.right 叔叔节点
                if (colorOf(y) == RED) {    // x.parent的兄弟节点y颜色为red(父节点和叔叔节点均为red)
                    setColor(parentOf(x), BLACK);   // x.parent.color = black
                    setColor(y, BLACK); // y.color = black
                    setColor(parentOf(parentOf(x)), RED);   // x.parent.parent.color = red
                    x = parentOf(parentOf(x));  // x = x.parent.parent 向上迭代检查(可能x.parent.parent.parent也为red)，注意此时x.parent.parent为red节点(当做新插入的节点)
                } else {    // x.parent的兄弟节点y颜色为black(父节点为red,叔叔节点为black)
                    if (x == rightOf(parentOf(x))) {    // x为右孩子
                        x = parentOf(x);    // x = x.parent
                        rotateLeft(x);  // 对x左旋(对插入节点x的父节点左旋)
                    }
                    // 插入节点x.parent与x.parent.parent互换颜色
                    setColor(parentOf(x), BLACK);
                    setColor(parentOf(parentOf(x)), RED);

                    rotateRight(parentOf(parentOf(x))); // 右旋
                }
            } else {    // 与上一种情况大体相似，些许差别
                // x.parent为右孩子 y = x.parent.parent.left
                Entry<K, V> y = leftOf(parentOf(parentOf(x)));
                if (colorOf(y) == RED) {    // x.parent的兄弟节点为red(父节点和叔叔节点均为red)
                    setColor(parentOf(x), BLACK);   // x.parent.color = black
                    setColor(y, BLACK); // y.color = black
                    setColor(parentOf(parentOf(x)), RED);   // x.parent.parent.color = red
                    x = parentOf(parentOf(x));  // x = x.parent.parent
                } else {
                    // x.parent 的兄弟节点为black(父节点为red,叔叔节点为black)
                    if (x == leftOf(parentOf(x))) { // x 为左孩子
                        x = parentOf(x);    // x = x.parent
                        rotateRight(x); // 对x右旋
                    }
                    // x.parent 和 x.parent.parent 互换颜色
                    setColor(parentOf(x), BLACK);   // x.parent.color = black
                    setColor(parentOf(parentOf(x)), RED);

                    rotateLeft(parentOf(parentOf(x)));  // 对x.parent.parent左旋
                }
            }
        }
        root.color = BLACK; // 头结点必须是BLACK
    }

remove

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
public V remove(Object key) {
        Entry<K, V> p = getEntry(key);
        if (p == null)
            return null;

        V oldValue = p.value;
        deleteEntry(p);
        return oldValue;
    }

    /**
     * Delete node p, and then rebalance the tree. 删除
     */
    private void deleteEntry(Entry<K, V> p) {
        modCount++;
        size--;

        // If strictly internal, copy successor's element to p and then make p
        // point to successor.
        if (p.left != null && p.right != null) {    // p有两个孩子
            // 找到p的后继s，s只有一个孩子，问题需要转变成删除节点至多只有一个孩子的问题
            // s可以直接顶替p的位置，问题就转化成删除s节点
            Entry<K, V> s = successor(p);
            p.key = s.key;
            p.value = s.value;
            p = s;
        } // p has 2 children

        // Start fixup at replacement node, if it exists.
        Entry<K, V> replacement = (p.left != null ? p.left : p.right);

        if (replacement != null) {  // 待删节点p有一个孩子
            // Link replacement to parent
            replacement.parent = p.parent;

            // p为头结点，孩子直接顶替即可
            if (p.parent == null)
                root = replacement;
            // p为左孩子
            else if (p == p.parent.left)
                p.parent.left = replacement;
            // p为右孩子
            else p.parent.right = replacement;

            // Null out links so they are OK to use by fixAfterDeletion.
            p.left = p.right = p.parent = null; // p的所有指针置空

            // Fix replacement
            if (p.color == BLACK)   // 只有待删节点为black才需要调整(少了个黑)
                fixAfterDeletion(replacement);
        } else if (p.parent == null) { // return if we are the only node.
            root = null;    // p就是头结点，删掉即可(没有dummyNode)
        } else { //  No children. Use self as phantom replacement and unlink.
            if (p.color == BLACK)   // 只有待删节点为black才需要调整
                fixAfterDeletion(p);

            // 将p的指针置空
            if (p.parent != null) {
                if (p == p.parent.left)
                    p.parent.left = null;
                else if (p == p.parent.right)
                    p.parent.right = null;
                p.parent = null;
            }
        }
    }

    private void fixAfterDeletion(Entry<K, V> x) {
        // 感叹一下，Josh Bloch and Doug Lea真是行走的逻辑机器。。。。

        // 从这里开始，是对上述删除节点的几种情况的完整概括，每个情况往下述逻辑里套，会发现以下代码的设计之巧妙
        while (x != root && colorOf(x) == BLACK) {
            // x == x.parent.left x为左孩子
            if (x == leftOf(parentOf(x))) {
                // x.parent.right 兄弟节点
                Entry<K, V> sib = rightOf(parentOf(x));

                if (colorOf(sib) == RED) {  // 兄弟节点为red，根据红黑树的条件，此时x x.parent sib.left sib.right 均为black
                    // 兄弟节点和父节点互换颜色
                    setColor(sib, BLACK);   // sib.color = black
                    setColor(parentOf(x), RED); // x.parent.color = red

                    rotateLeft(parentOf(x));    // 对x.parent左旋
                    sib = rightOf(parentOf(x)); // sib = x.parent.right 为black, 兄弟节点产生了变化(为左旋前的sib.left变为父节点的右子树，即x的兄弟节点)
                }

                // 兄弟节点sib为black

                if (colorOf(leftOf(sib)) == BLACK &&    // 兄弟节点左子树为black
                        colorOf(rightOf(sib)) == BLACK) {   // 兄弟节点右子树为black
                    // 即兄弟节点，及兄弟左右孩子均为黑
                    setColor(sib, RED); // 将兄弟节点变为red
                    x = parentOf(x);    // x = x.parent
                } else {    // 兄弟节点sib至少有一个孩子为red
                    if (colorOf(rightOf(sib)) == BLACK) {   // sib.right.color == black
                        // 此时sib.left.color == red

                        // sib 和sib.left互换颜色
                        setColor(leftOf(sib), BLACK);   // sib.left.color = black
                        setColor(sib, RED); // sib.color = red

                        rotateRight(sib);   // 对sib右旋
                        sib = rightOf(parentOf(x)); // 兄弟节点sib = x.parent.right
                    }
                    //
                    setColor(sib, colorOf(parentOf(x)));    // sib和x.parent互换颜色
                    setColor(parentOf(x), BLACK);
                    setColor(rightOf(sib), BLACK);
                    rotateLeft(parentOf(x));    // 对x.parent左旋
                    x = root;   // 跳出
                }
            } else { // symmetric
                // 跟上边呈完全对称

                Entry<K, V> sib = leftOf(parentOf(x));

                if (colorOf(sib) == RED) {
                    setColor(sib, BLACK);
                    setColor(parentOf(x), RED);
                    rotateRight(parentOf(x));
                    sib = leftOf(parentOf(x));
                }

                if (colorOf(rightOf(sib)) == BLACK &&
                        colorOf(leftOf(sib)) == BLACK) {
                    setColor(sib, RED);
                    x = parentOf(x);
                } else {
                    if (colorOf(leftOf(sib)) == BLACK) {
                        setColor(rightOf(sib), BLACK);
                        setColor(sib, RED);
                        rotateLeft(sib);
                        sib = leftOf(parentOf(x));
                    }
                    setColor(sib, colorOf(parentOf(x)));
                    setColor(parentOf(x), BLACK);
                    setColor(leftOf(sib), BLACK);
                    rotateRight(parentOf(x));
                    x = root;
                }
            }
        }

        // 跳出循环时，要么x为root，要么x.color=red,两种情况都应该置x.color=black
        setColor(x, BLACK);
    }

小结

  • TreeMap为一种有序的Map
  • 有序的保证来自于内部元素的组织依托于红黑树
  • 因为内部是红黑树实现，所以 put get 等操作的时间复杂度为log(n)
-------------The End-------------